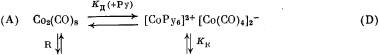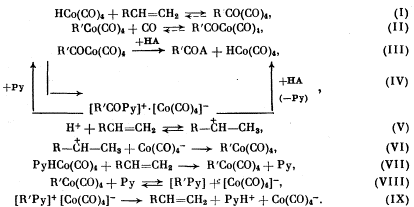Карта сайта

КАТАЛИТИЧЕСКАЯ СИСТЕМА КАРБОНИЛЫ КОБАЛЬТА - ПИРИДИН В РЕАКЦИЯХ КАРБОНИЛИРОВАНИЯ ОЛЕФИНОВ

МОДЕЛИРОВАНИЕ ВЛИЯНИЯ ПИРИДИНА НА КИНЕТИКУ РЕАКЦИИ АЛКОКСИКАРБОНИЛИРОВАНИЯ

© 1992 г. В.Н. ДОГАДАЕВ,
А.И. ГРИГОРЬЕВ,
Г.Н. ГВОЗДОВСКИЙ
Рассмотрены альтернативные варианты механизмов реакций карбонилирования олефинов с учетом равновесий в каталитической системе карбонилы кобальта - пиридин с точки зрения их соответствия основ­ным наблюдаемым закономерностям. Предложены кинетические моде­ли, отражающие различные пути активации олефина как лимитирую­щей стадии, проведена их дискриминация по зависимостям начальных скоростей реакции карбонилирования октена-1 в этиленгликоле от концентраций кобальта и пиридина. Показано, что наиболее вероятна с ки­нетической точки зрения модель, в которой каталитически активной частицей является пиридинкобальтгидрокарбонильный молекулярный комплекс.
Каталитическая система гидрокарбонил кобальта — пиридин проявляет высокую эффективность в реакциях получения сложных эфиров и карбоновых кислот методами алкокси- и гидроксикарбонилирования олефинов и диолефинов [1-3]. Так как данные методы имеют важное прикладное значение, большое количество исследований посвящено изучению влияния параметров этих реакций на их скорость и селективность. Однако ряд наблюдаемых закономерностей, отражающих специфику действия пиридина, не имеет пока адекватного количественного описания и в различных работах [3-8] трактуется по-разному.
С целью определения схемы реакций, наиболее точно описывающей экспериментальные зависимости с учетом механизма взаимодействия пиридина с карбонилами кобальта в ходе процесса карбонилирования, нами была изучена кинетика реакции карбонилирования октена-1 в этиленгликоле при варьировании концентраций кобальта и пиридина, составлены альтернативные кинетические модели процесса, проведена идентификация параметров и дискриминация моделей.
На основании результатов большого числа спектроскопических и дру­гих исследований системы карбонилы кобальта—пиридин [8-11], с точ­ки зрения современных представлений о механизмах сольватации и кис­лотно-основного взаимодействия [12], может быть рассмотрена следующая упрощенная схема равновесий, характеризующая данную каталитическую систему:

Упрощенная схема равновесия для данной каталитической системы

Упрощенная схема равновесия для данной каталитической системы

В присутствии пиридина, как было показано в [8], равновесие сильно сдвинуто в сторону форм (D) и (Е), при этом общепризнано, что анион Со(СО)4-- в условиях реакций карбонилирования олефинов каталитически неактивен, так же как и дикобальтоктакарбонил (А), который лишь выполняет роль определенного резервуара кобальта в системах без пиридина [7]. Альтернативные механизмы реакций карбонилирования приведены ниже:

Механизм процессов карбонилирования базируется на классической схеме Бреслоу—Хека [13], включающей в себя три основные стадии ((I)—(III)) с гидрокарбонилом кобальта (В) в качестве каталитически активной частицы. При изучении влияния пиридина на относительные ско­рости стадий в работе [14] было показано, что стадия (III) распада ацилкобальткарбонила в присутствии уже стехиометрических количеств пиридина ускоряется более чем в 400 раз, проходя через образование тетракарбонилкобальта N-ацилпиридиния по маршруту (IV). По данным [4], при добавлении пиридина изменяются наблюдаемые порядки реакции по олефину — от 0 до 1 и по спирту — от 1 до 0, что свидетельствует о смене лимитирующей стадии от реакции (III) в системе без пиридина к реакции (I) в его присутствии.
В исследованиях работы [8] был развит предложенный в [15] механизм, согласно которому лимитирующей стадией процессов карбонилирования является активация олефина протоном (С), идущая через образование карбкатиона по реакциям (V), (VI).
При качественном анализе с формально-кинетических позиций механизмов Бреслоу — Хека и Мирбаха по схеме (I)—(IХ) с учетом схемы равновесии наблюдается определенное несоответствие описания экспериментальным данным. Так, в работе [4] было показано, что зависимость скорости реакции метоксикарбонилирования гексена-1 от концентрации пириди­на имеет экстремальный характер с максимумом скорости в области концентрации пиридина Сп=4—6 моль/л, при этом мольное отношение кон­центраций пиридина и кобальта Сп/Ск=60-100. Однако в соответствии с принятыми схемами при увеличении отношения Сп/Ск выше стехиометрического и лимитирующей первой стадии скорость реакции должна монотонно понижаться с увеличением концентрации пиридина в реакционной смеси как при катализе гидрокарбонилом кобальта (В) по механизму Бреслоу — Хека, так и при активации протоном (С) по схеме Мирбах в связи со смещением равновесии в сторону каталитически неактивной системы (F) и недиссоциированной системы (Е).
С учетом изложенного в качестве альтернативы рассмотренным механизмам может быть принята гипотеза о катализе реакций карбонилирования олефинов системой (Е) [16], представляющей собой пиридинкобальт-гидрокарбонильный молекулярный комплекс с переносом протона [17, 18]. Данное предположение явно не противоречит наблюдаемым кинетическим закономерностям, поскольку указанная каталитическая система (Е) в соответствии с приведенной схемой равновесий должна стабилизироваться определенным избытком пиридина. Реакция активации олефина при ката­лизе комплексом (Е) описывается в общем виде уравнением (VII), при этом возможно участие пиридина в обратной реакции превращения алкилкобальткарбонилов в исходные реагенты через образование четвертичной соли N-алкилпиридиния с последующим элиминированием по реакциям (VIII) и (IX).
Количественная оценка соответствия обсуждаемых механизмов процесса карбонилирования экспериментальным данным осуществлялась по детерминированным кинетическим моделям, отражающим совокупность равновесной и кинетической схем, и разработанным с учетом предпосылки о лимитирующей стадии взаимодействия олефина с каталитически активной формой катализатора. При этом наблюдаемые порядки реакции по олефину и спирту соответствовали экспериментально определенным, а концентрации интермедиатов — алкил- и ацилкобальткарбонилов — могут рассматриваться в квазистационарных приближениях.
Структура кинетических моделей в общем виде выражается системой уравнений, полученной при формально-кинетическом описании схемы (I) - (IХ):

W= ─dCол/dτ=Скт/(Kn1+Kn2Cn), (1)

Кп2=0, (2)

где Скт - концентрация активной формы катализатора для соответствующей модели; Kn1, Кn2 — нелинейные параметрические функции (НПФ) от кинетических констант элементарных стадий Ki и действующих концентраций реагентов олефина, спирта и окиси углерода: (Сол, Ссп,Рсо).
Условие (2) действительно для случаев, когда лимитирующая стадия процесса рассматривается как необратимая либо обратимая без участия пиридина, т. е. без учета реакций (VIII) и (IX).
Концентрация компонентов равновесной системы карбонилы кобальта — пиридин, в том числе каталитически активных форм Cкт (гидрокарбонила кобальта, протона и пиридинкобальтгидрокарбонильного молекулярного комплекса), определяющих возможность протекания реакции по одному из трех приведенных механизмов, были выражены в соответствии с приведенной выше схемой равновесий и материальным балансом по кобальту и пиридину.
В результате после некоторых упрощений с учетом относительных значений констант ионизации гидрокарбонила кобальта и катиона пиридиния [18, 19] имеем уравнения для концентрации Cкт в явном виде:

  1.  гидрокарбонил кобальта: Снк=КнкСк/Сп (3)
  2.  протон: Cн=Knр(Cк/Cп) (4)
  3.  пиридинкобальтгидрокарбонильный молекулярный комплекс: Cпк=KпкCпCк/(Сп+Кпк) (5)

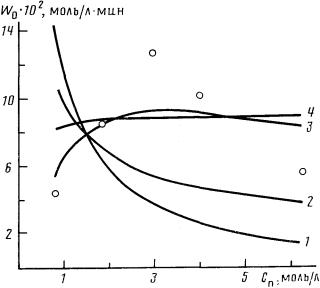
Экспериментальные (точки) и рассчитанные по моделям зависимости начальной скорости реакции алкоксикарбонилирования октена-1 в этиленгликоле от концентрации пиридина (Сол° = 1,67 моль/л, Ссп° = 1,67 моль/л, Ск = 0, 11 моль/л, растворитель — толуол, 160°, Рсо = 15 • 106 Па): 1 - модели 1, 2; 2 - 3, 4; 3 - 5; 4 - 6
Рис. 1. Экспериментальные (точки) и рассчитанные по моделям зависимости начальной скорости реакции алкоксикарбонилирования октена-1 в этиленгликоле от концентрации пиридина (Сол° = 1,67 моль/л, Ссп° = 1,67 моль/л, Ск = 0, 11 моль/л, растворитель — толуол, 160°, Рсо = 15 • 106 Па): 1 - модели 1, 2; 2 - 3, 4; 3 - 5; 4 - 6

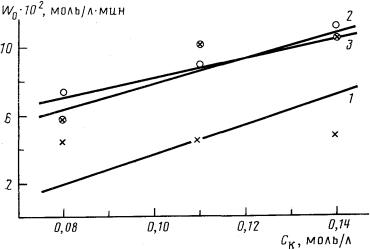
Влияние концентрации кобальта на начальную скорость реакции алкоксикарбонилирования октена-1 в этиленгликоле (Сол0 = 1, 67 моль/л, Cсп° = 1, 67 моль/л, растворитель — толуол, 160°, Рсо = 15 • 106 Па) при различных значениях Сп: 1 — 0, 9; 2 — 1, 8; 3 — 4, 0 моль/л
Рис. 2. Влияние концентрации кобальта на начальную скорость реак­ции алкоксикарбонилирования октена-1 в этиленгликоле (Сол0 = 1, 67 моль/л, Cсп° = 1, 67 моль/л, растворитель — толуол, 160°, Рсо = 15·106 Па) при различных значениях Сп: 1 — 0,9; 2 — 1,8; 3 — 4,0 моль/л

где Кнк, Кпр, Кпк, Кпк' — приведенные константы равновесия для соответствующих компонентов каталитической системы.
После подстановки выражений для равновесных концентраций (3) — (5) в кинетическое уравнение (1) получены шесть кинетических моделей процесса карбонилирования, отражающих механизмы Бреслоу — Хека, Мирбах, и катализа молекулярным комплексом, каждая соответственно для двух предложенных вариантов кинетического уравнения (системы (1) и (2)).

Статистические характеристики альтернативных моделей

Модель Катализатор Уравнения n ∑ri2 Fэксп ∑табл η
1 НСо(СО)4 (1), (3) 2 64,6 26,8 4,71 1,8·10-63
2 НСо(СО)4 (1) - (3) 1 64,6 26,8 4,68 1,8·10-63
3 Н+ (1), (4) 2 33,8 14,1 4,71 5,0·10-30
4 Н+ (1), (2), (4) 1 33,8 14,1 4,68 5,0·10-30
5 PyHCo (СO)4 (1), (5) 3 6,81 3,39 4,74 1
6 РуНСо(СО)4 (1), (2), (5) 2 12,5 5,65 4,71 6,6·10-7

Обозначения: n — число параметров, ∑ ri2 — сумма квадратов отклонений, F — критерий Фишера, η — критерий отношения вероятностей.

Для каждой из полученных моделей проводили оценку параметров и их погрешностей методом минимизации суммы квадратов отклонений экспериментальных и расчетных значений скоростей реакции, проверка на адекватность и дискриминация моделей по критерию Фишера и критерию отношений вероятностей [20, 21].
Ввиду того, что кинетические параметры моделей нелинейно зависят от текущих концентраций олефина и спирта и давления оксида углерода, а также в связи с параллельно протекающей реакцией изомеризации исходного олефина по двойной связи, идентификация моделей осуществлялась по зависимости начальных скоростей реакции от концентраций пиридина и кобальта в реакционной смеси при одинаковых начальных условиях. Значения начальных скоростей определялись методом численного дифференцирования в исходной точке кинетической кривой изменения концентрации олефина.
На рис. 1 и 2 представлены результаты экспериментов по изучению влияния концентраций пиридина и кобальта на начальные скорости реак­ции и кривые зависимостей, рассчитанные для альтернативных моделей. Полученные данные согласуются с результатами аналогичных работ [4, 22], при этом характер кривых полностью подтверждает выводы, сделан­ные при качественном анализе кинетических схем реакции. Статистические характеристики адекватности моделей, приведенные в таблице, количест­венно отражают степень соответствия описаний наблюдаемым закономер­ностям (определены для дисперсии воспроизводимости результатов, равной 2·10-4).
Из шести рассмотренных моделей адекватной по критерию Фишера является только модель 5 (см. таблицу), описывающая кинетику реакции карбонилирования с участием пиридинийкобальткарбонильного молекулярного комплекса и пиридина в обратимой лимитирующей стадии активации олефина по реакциям (VII)—(IX). Критерий отношения вероятностей для этой модели значительно превосходит критерии, рассчитанные для остальных моделей, и составляет ~1.
Структура данной модели может быть выражена в следующем виде:

W0 = СкСп/(a0+a1Cп + а2Сп2), (6)

где ai — наблюдаемые кинетические параметры модели, включающие в себя кинетические НПФ и приведенные константы равновесия. Рассчитанные МНК оптимальные оценки указанных параметров и их дисперсии равны a0 = 1,1(0, 6); a1=0,5 (0,6); a2=0,1 (0,2).
Следует отметить, что только кинетическая модель 5 в отличие от остальных имеет решение для первой производной по пиридину, приравненной к нулю (соответствующей виду функции с экстремумом). Более резкое снижение экспериментальных значений начальных скоростей в области больших концентраций пиридина по сравнению с расчетными можно, по-видимому, объяснить образованием неактивных полипиридинзамещенных комплексов [9, 22] либо связыванием катиона пиридиния в комплексы типа Ру2Н+ [8, 17]. Включение в модель взаимодействий такого типа должно несколько усложнить ее и одновременно повысить точность описания экспериментальных данных.
Таким образом, методом моделирования кинетики реакции алкоксикарбонилирования олефинов, включающей пиридин на стадии активации и в равновесных реакциях с карбонилами кобальта, показано, что с наибольшей степенью вероятности наблюдаемым закономерностям соответствует механизм катализа пиридинкобальтгидрокарбонильным молекулярным комплексом.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

В реактор объемом 1 л загружали смесь этиленгликоля, толуола и катализатора и выдерживали при перемешивании в течение 1 ч при задан­ных температуре и давлении с целью установления равновесия каталити­ческой системы. Реакцию начинали передавливанием октена-1 в реактор. Катализатор получали по методике [23], при этом ИК-спектр системы, снятый в условиях реакции, имел только характерную полосу 1900 см-1, соответствующую аниону Со (СО)4¯, и отношение содержания активного кобальта к общему, определенное по методике [24], равнялось 1. Значения давления и температуры при проведении реакции поддерживали с точностью = ±2%. Через заданный промежуток времени реакцию останавливали путем резкого охлаждения реактора, пробы анализировали мето­дом газожидкостной хроматографии.
 
СПИСОК ЛИТЕРАТУРЫ
  1. Гвоздовский Г.Н. , Гаврилова В.М., Догадаев В.Н. // Процессы нефтепереработки и нефтехимии. Ч. 1. М.: ЦНИИТЭиефтехим, 1989. С. 146.
  2. Бланштейн И. Б., Гаврилова В. М., Гвоздовский Г. Н, Рыбаков В. А. // Процессы нефтепереработки и нефтехимии. Ч. I. М.: ЦНИИТЭнефтехим, 1989. С. 133.
  3. Имянитов Н.С. // Кинетика и катализ. 1987. Т. 28. № 4. С. 829.
  4. Кацнельсон М. Г. // Жури. прикл. химии. 1973. Т. 46. № 12. С. 2745.
  5. Кацнельсон М Г. // Журн. прикл. химий. 1974. Т. 47. № 1. С. 155.
  6. Боровиков М.С., Рыбаков В А. // Кинетика и катализ. 1985. Т. 26. № 4. С. 837.
  7. Боровиков М.С., Рыбаков В.А. // Кинетика и катализ. 1986. Т. 27. № 2. С. 319.
  8. Mirbach М.F; Mizbach Н.J. // J. Molec. Catalysis. 1985. V. 32. N 1. Р. 59.
  9. Боровиков М.С, Рыбаков В.А., Тарасов Б.Я. // Физико-химические аспекты разработки нефтехимических процессов. М.: ЦНИИТЭнефтехим, 1983. С. 16.
  10. Боровиков М.С. и др. // Журн. общ. химия. 1982. Т. 62. № 2. С. 331.
  11. Rybakov V.A., Gvozdovskij G. N., Gavrilova V.М. // Fundamental Research in Ho­mogeneous Catalysis. V. 3. N. Y.: Gordon L Breach, 1986. P. 1149.
  12. Фиалков Ю.Я. // Растворитель как средство управления химическим процессом. Л.: Химия, 1990. С. 12.
  13. Heck R.F., Breslow D.S. // J. Amer. Chem. Soc. 1961. V. 83. N 19. Р. 4023.
  14. Имянитов Н.С, Богорадовская Н.М., Семенова Т.А. // Кинетика и катализ. 1978. Т. 19. № 3. С. 573.
  15. Natta G., Pino P., Mantica E. // Gazz. Chim. Ital. 1950. A. 80. P. 680.
  16. Шелдон Р.А. // Химические продукты на основе синтез-газа. М.: Химия, 1987. С. 107,
  17. Зегерс-Эйскенс Т. и др. // Молекулярные взаимодействия. М.: Мир, 1984. С. 11.
  18. Имянитов Н.С. // Координац. химия. 1986. Т. 12. № 3. С. 309.
  19. Альберт А., Сержент E. // Константы ионизации кислот и оснований. М.: Химия, 1964. С. 140.
  20. Горский В.Г. // Планирование кинетических экспериментов. М.: Наука, 1984. С. 157.
  21. Reilly P.М. // Canad. J. Chem. Engng. 1970. V. 40. N 2. Р. 169.
  22. Hofmann P., Kasswig К., Schaefer W. // Industr. and Engng Prod. Res. Dev. 1980. V. 19. N 3. Р. 330.
  23. Потатуев А.А., Рыбаков В.А., Юров В.В. и др // Тез. докл. VI Всесоюз. конф. по поверхностно-активным веществам и сырью для их производства. Волгодонск, 1984. С. 428.
  24. Wender I., Sternberg Н. W., Orchin М. // Analyt. Chem. 1952. V. 24. N 1. Р. 174.
Счетчики и кнопки
Э-Хим.Нефтехимические технологии Яндекс.Метрика Рейтинг@Mail.ru ОПТИМА СЕРТ. Сертификационный Центр